When signing up for an email or to a website do you remember the exhausting procedure of selecting a username? First, you try with something simple like your first name or last name. Unless you have a really unique name, good luck with that. Next, you append your birth year to it. Still no luck? I am sure you have tried adding your phone number too. By this time, you already start loathing your username.

We can only try so many usernames, and we feel mentally exhausted. Imagine what goes under the hood. For each username you try, the computer must check against all the username it has stored in its database. And for applications such as Facebook, Twitter, and Instagram, the task is a challenge in itself.

How do you think these social media giants with hundreds of millions of users manage to check if a username is available or not and within milliseconds inform you? Clearly simple solutions like linear search are inefficient. Well, one possible optimal solution is the use of Bloom Filter.

What is Bloom Filter?

Bloom Filter is a probabilistic time and space efficient data structure used to represent a set and perform membership queries i.e. query whether an element is a member of the set or not. Burton H. Bloom first purposed bloom filter in his paper Space/Time Trade-offs in Hash Coding with Allowable Errors in 1970.

There are two parts to a Bloom Filter:

• Bit Vector
• Hash Function

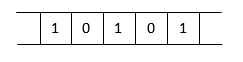
Bit Vector

A bit vector is an array of n x 1 dimensions consisting of either 1 or 0 as its member. All the bit values are first initialized to 0.

Hash Function

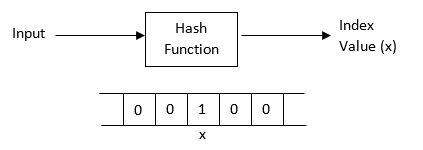
A hash function takes an input and generates a fixed-bit-size hash code. Here in our case, we use the hash function to generate an index value for the bit vector.

Here is how the two combine to implement bloom filter.

For every member (username), to be stored in the bit vector, it must first pass through the hash function. The hash function generates a hash code or index value. The bit value at the corresponding index of bit vector is set to 1. We can use multiple hash functions as well which will alter the bit at that many index positions.

Now, if we want to check whether a member (username) is in the bit vector or not, we simply pass it through the hash function and generate an index value. Next, we check the bit value at that index position. If the value is 1, the member is in the bloom filter, else it is not.

The Probabilistic Part

Bloom Filter is called a probabilistic data structure and here is the reason why.

When we query the membership of an element into a bloom filter one of two results is possible. Either the member is not present i.e. get 0 as the return value or the member is present i.e. get 1 as return value at the index position generated by the hash function.

When we get a 0 as the return value, it signifies that the element is definitely not present in the bloom filter. However, if we get a 1 as the return value, it does not guarantee that the element is present in the bloom filter. It signifies that the element may be present. The reason behind it is the use of the hash function.  A hash function maybe collision-prone i.e. the hash function may generate same index value even for different members. As a result, the hash function may generate an index value at which the bit value is already 1. Hence, even though the member is not present in the bloom filter, the result will be that the member is already present. This is the case of false positive.

False positives in bloom filter can be minimized by using bit values at multiple positions to represent a single element. One of the ways of achieving it is the use of multiple hash functions. Or we can use a hash function with good uniform distribution.

Bloom Filter is a simple and elegant solution for membership queries.

Time Efficiency

Bloom Filter implements the concept of indexing which has a time complexity of O(1). If we use k number of hash functions, it becomes O(k).

Space Efficieny

The most attractive feature of a bloom filter is its space efficiency. All that a bloom filter stores are bit values. One member is represented by a single bit value. Hence, we can store billions of members in a bloom filter that takes only a few hundred MB of memory. As a result, we can store the data even in primary memory for fast access.

Detecting Duplicate Username While Registration using a Bloom Filter

Now that we are clear what a bloom filter is, how it works, and what its advantages are, let’s implement it in detecting duplicate username while registering to a dummy email application.

We will implement it using Node.js and we will use Redis database to implement the bit vector and use Murmur hash function.

Part I: Bit Vector using Redis Database

Redis is an open-source in-memory database that stores data in memory rather than hard disk which means database query is faster.

Redis supports different types of data structures such as string, sets, bit set etc. We will use the bitmap data structure to implement the bit vector. Redis implements the bitmap using its string data structure i.e. it stores the bit vector as a string.

The string is capable of storing 32 bits while occupying a memory space of just 512 MB. That means to store 4 billion members, it will only occupy 512 MB of space.

The bitmap has two function calls:

• setbit: to set bit value to 1 at specified index position
• getbit: to get the bit value at specified index position

Part II: Hash Function using MurmurHash

We are using a 32-bit version MurmurHash function. We will install the MurmurHash3js module and call murmurHash3.x86.hash32(string) function. 

We are using the MurmurHash function because it is an excellent choice for hash-based lookups.  In a test conducted by Colin Pesyna, Murmur hash function was found to have no collision while testing with 42 million keys. Further tests concluded that MurmurHash function had random uniform distribution and good avalanche effect. All these properties make Murmur hash an excellent choice for use in bloom filter.

Part III: Implementation in Registration Logic

First, we check if the username is available or not.

If the username is available, then we allow registration. First, enter the user details in the database and then set the bit value corresponding to the username to 1.

Screenshots

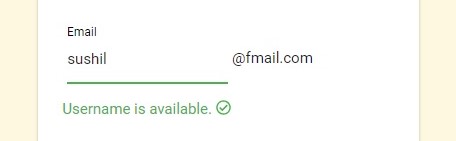Case I: Username is available

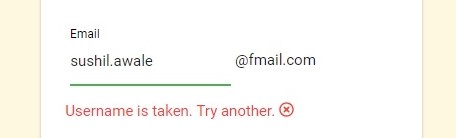Case II: Username is not available

You can find the full project on my GitHub account.

Bloom Filter is such a versatile data structure. There are many more variants of the data structure and it has a wide range of applications in networking, security, big data. Here is a good resource that highlights just that.